[TIL] 시계열 데이터
A. 시계열 데이터(Time Series Data)
1. 정의
시간에 따라 정렬된 데이터로, 주기적으로 기록되어 이를 동일한 시간단계(timestep)로 분포한다고 정의한다.
시계열은 추세, 계절성, 잔차로 분해된다.
2. 추세(Trend)
지속적이고 일관된 방향으로 변화하는 장기적 패턴을 의미한다.
시계열에서 느리게 움직이는 큰 변화를 나타낸다. 시간이 지남에 따라 시계열이 점진적으로 증가하거나 감소하는 현상을 말한다.
3. 계절성(Seasonality)
일정한 시간 주기에 따라 반복되는 패턴으로, 일반적으로 시간에 관련된 고정된 주기를 가지고 있으며 특정시점에서 데이터가 규칙적으로 상승하거나 하락하는 현상을 말한다. 사계절을 의미하는 것이 아니라 순환하는 현상을 이야기한다.
4. 주기성(Cycles)
경제적, 사회적, 정치적 요인에 의해 발생하는 불규칙한 변동 패턴으로 장기적으고 불규칙한 패턴이다.
계절적 구성요소는 시계열의 계절적 패턴, 주기는 일정 기간 동안 반복적으로 발생한다.
| 개념 | 계절성 | 주기 |
| 규칙성 | 일정한 간격으로 반복 | 불규칙적으로 발생 |
| 발생 원인 | 계절적 요인(기후 등) | 경제, 사회적인 요인(경기순환) |
| 시간 범위 | 1년 이내 | 수년 이상 |
5. 잔차(Residual)
시계열 데이터에서 추세와 계절성을 제거한 후 남는 무작위적 변화량을 의미한다. 특정 패턴을 가지지 않으며 주로 백색소음(White Noise)처럼 랜덤한 요소이다.
6. 시계열 예측 vs 회귀 예측
| 머신러닝 모델 | 시계열 모델 | |
| 종속변수(Y) | 수치형, 범주형 | 주로 수치형 |
| 독립변수(X) | 다중 변수 가능 | 단일 변수(주로 시간) |
| 모델 유형 | 선형회귀, 의사결정나무, 신경망 등 | ARIMA, Prophet 등 |
| 장점 | 여러 변수간의 관계를 분석 가능 비선형 패턴 학습 기능 |
시간의 흐름 포착 기능 이해와 해석이 용이 |
| 단점 | 시간에 따른 의존성 무시(추세, 계절성) 과적합 위험 |
다변량 분석 제한 비선형 모델링 제한 |
| https://snowgot.tistory.com/120 | ||
B. 확률 보행(Random Walk) 프로세스
1. 확률보행 정의
평균과 분산이 시간이 지나도 일정하지 않은 비정상 시계열로, 시간이 지남에 따라 무작위로 이동하는 경로를 설명하는 수학적 모델이다. 공식은 아래와 같다.

현재 값은 과거 값, 상수, 백색소음의 입력값으로 결정된 함수이며, 현재 값이 과거 정보와 랜덤한 변동의 영향을 받는다.
C. 정상성(Stationarity)
1. 정상성의 정의
시계열의 통계적 성질이 시간에 따라 변하지 않는 상태를 의미한다. 시계열 데이터에서 정상성을 가정하거나 내포하면 모델링과 예측 가능성이 좋아진다. 통계적 성질이란 데이터의 중앙값, 분포, 변동성, 상관성 등의 특성을 나타내며 데이터를 분석하는데 있어 중요한 역할을 한다.
Nelson-Plosser의 연 평균 물가상승률 데이터를 통해 알아보고자 한다.
# 연도별 평균 물가 상승률 계산
import statsmodels.api as sm
import pandas as pd
import matplotlib.pyplot as plt
data = sm.datasets.macrodata.load_pandas().data
inflation_rate_df = pd.DataFrame({
'Year': data['year'],
'Inflation Rate': data['infl']
})
inflation_rate_yearly_avg = inflation_rate_df.groupby('Year').mean().reset_index()
# 데이터프레임 출력
display(inflation_rate_yearly_avg.loc[:5,:])
# 연도별 평균 물가 상승률 시각화
plt.figure(figsize=(10, 5))
plt.plot(inflation_rate_yearly_avg['Year'], inflation_rate_yearly_avg['Inflation Rate'], label='Average Inflation Rate')
plt.title('Average Inflation Rate per Year')
plt.xlabel('Year')
plt.ylabel('Inflation Rate')
plt.grid(True)
plt.show()
2. 정상성 시계열 조건
1) 시계열의 평균이 시간에 따라 변하지 않고 일정함
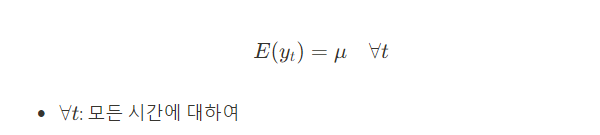
시간이 변해도 데이터가 일정한 평균 주위를 중심으로 변동한다고 볼 수 있다.

2) 시계열의 분산이 시간에 따라 일정함
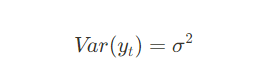
시간에 관계없이 일정한 변동성을 갖는다.
3) 시계열의 두 시점간 공분산이 시간(t)에 의존하지 않고 시간의 차(h)에만 의존함
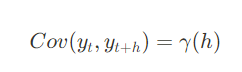
공분산은 두 확률 변수의 선형 관계를 나타내는 값이며, 시점 t의 데이터와 t+h 시점의 데이터 사이의 공분산이 시간 t에 무관하게 일정하다는 의미를 갖는다.
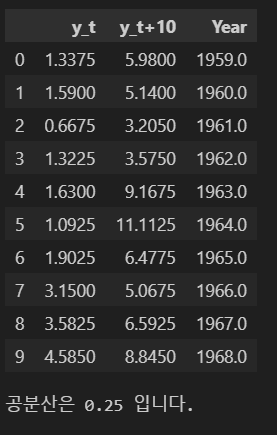
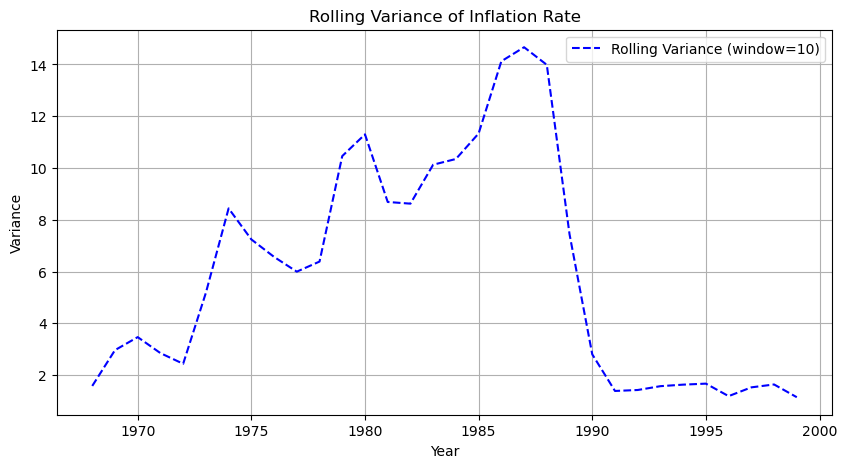
3. 정상성 확보를 위한 데이터 변환 기법
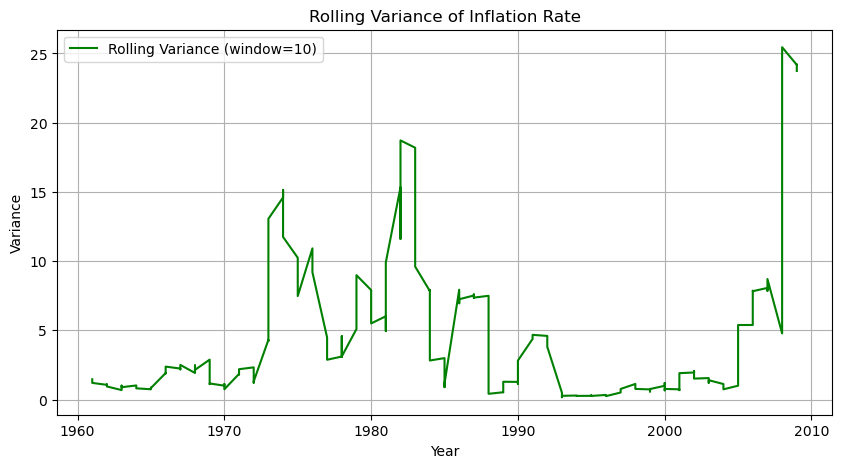
1) 위의 데이터는 평균, 분산, 공분산이 모두 변동하고 있으며, 이는 비정상성을 띈다고 볼 수 있다.
2) 평균 안정화
- 차분(Diffencing)
추세, 계절성을 제거하기 위한 방법으로, 특정 시점과 그 시점 사이 발생하는 변화를 계산한다.
- 이동 평균 평활화(Moving Average Smoothing)
단기적인 변동성을 제거하고 전체적인 추세를 더 명확히 볼 수 있다.
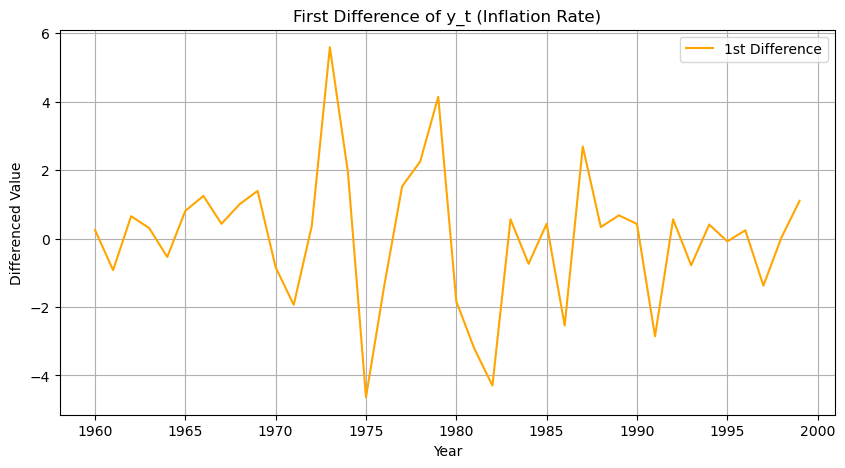
3) 분산 안정화
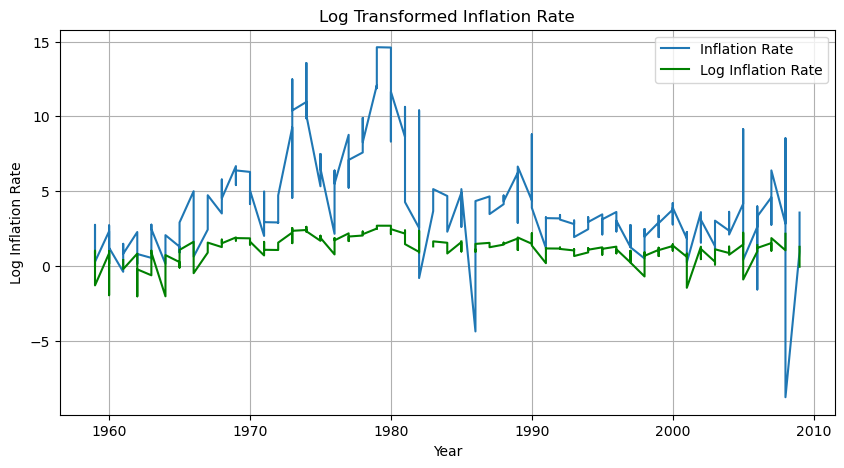
- 로그 변환
분산을 줄이기 위한 변환으로, 데이터의 스케일이 너무 커지거나 변동성이 큰 경우 유용하다.
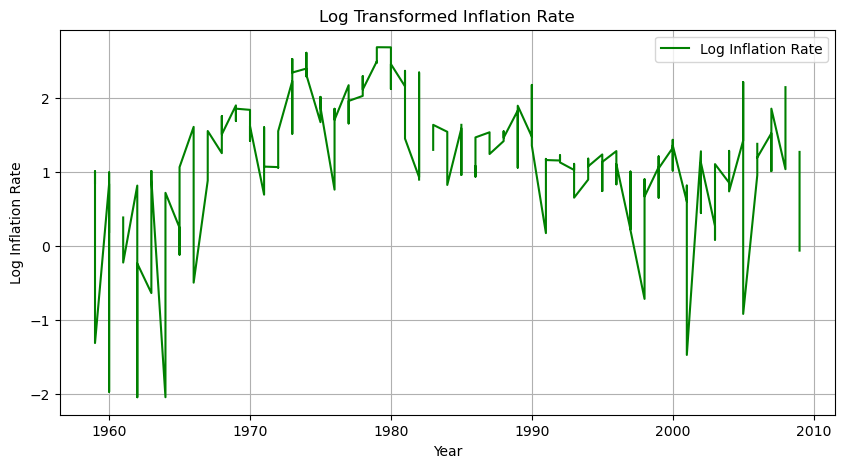
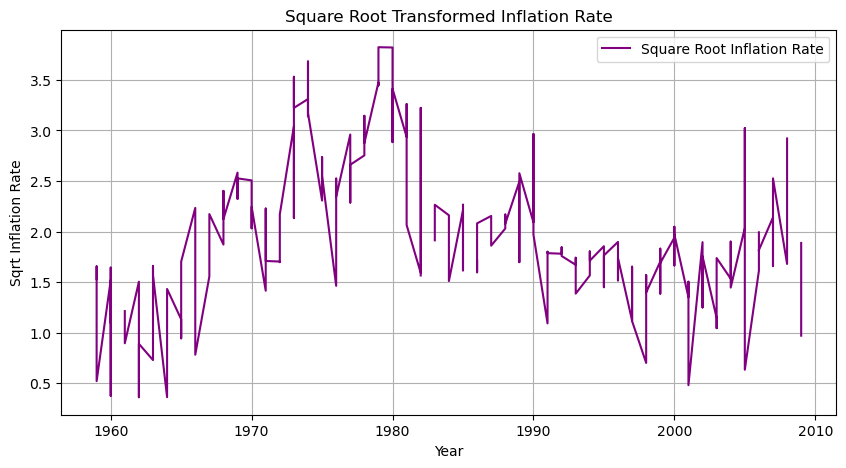
- 제곱근 변환
로그효과와 유사하게 분산을 줄이는 효과가 있으며 데이터가 극단적으로 변동하는 경우 유용하다.
D. 마무리
계속해서 비정상성을 나타낸다.
E. 20240926 내용 추가
정상성 확보를 위한 데이터 변환 기법을 사용하였음에도 불구하고 비정상성을 나타내는 것 같아 기존 그래프와 비교하였다.
1. 차분 적용

2. 로그 변환
3. 제곱근 변환

각 방법을 사용하였을 때 확실히 이 전보다 정상성을 갖는 것을 확인할 수 있다.
전에 그린 그래프의 Y축 값이 일정하지 않았기 때문에 그래프가 계속 널뛰는 것처럼 보였던 것이었다. 그래프를 그리면 축 확인하자.
해당 데이터는 분산 안정화를 시켰을 때 정상성을 갖는 것으로 보인다. 그 이유가 궁금해진다.